OK, time for a little math walk. Imagine that Bolzano's grocery is running a special on Weirstrass' Premium Vegan Schnitzel. People start converging on the corner in front of Bolzano's from all around. Based on counts using awesome new really big data technology, the local news media makes the amazing announcement that there are infinitely many people in the city block around Bolzano's. The subject of this walk is showing that there must be at least one location in that block where you can't move even the slightest distance without bumping into someone.
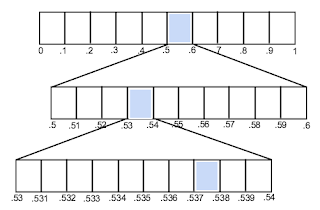
To simplify things, lets smash everything down into one dimension and pretend that the city block above is the closed interval $[0, 1]$ on the real number line. Let's represent the infinite set of people as points in this interval. Now consider the subintervals $(0, .1), (.1, .2), ... (.9, 1).$ At least one of these intervals must contain infinitely many people. Suppose, for example, that the interval $(.5, .6)$ contains infinitely people. Then split that interval into 10 segments, as shown in the picture below. At least one of these has to contain infinitely many people. Suppose, again for example, that this subinterval is $(.537, .538)$.
Now consider the number .537. We know that there are infinitely many people within .001 of .537. There is nothing stopping us from continuing this process indefinitely, finding smaller and smaller subintervals with left endpoints $.5, .53, .537... $ each containing infinitely many people. Let $r$ be the number whose infinite decimal expansion is what we end up with when we continue this process ad infinitum. To make $r$ well-defined, let's say that in each case we choose the left-most subinterval that contains infinitely many people. Depending on how the people are distributed, $r$ might be boring and rational or something exotic like the decimal expansion of $\pi$. The point is that it is a well-defined real number and it has the property that no matter how small an interval you draw around it, that interval includes infinitely many people. This is true because for each $n$, the interval starting at $r$ truncated to $n$ decimal digits and ending $1 / 10^n$ higher than that contains both $r$ and infinitely many other people by construction. In the example above, for $n = 3$, this interval starts at $.537$ and ends at $.538$.
Now let's remove the simplification, one step at a time. First, let's see how the same construction works if in place of $[0, 1]$ we use any bounded interval $[a, b]$. Consider the function $f(x) = (x - a) / (b - a)$. That function maps $[a, b]$ onto $[0, 1]$. Its graph is a straight line with slope $1/(b - a)$. If $b - a$ is larger than 1, points get closer together when you do this mapping; otherwise they get further apart. But the expansion or contraction is by a constant factor, so the picture above looks exactly the same, just with different values for the interval endpoints. So if we do the construction inside $[0, 1]$ using the mapped points, then the pre-image of the point $r$ we end up with will be an accumulation point for the set in $[a, b]$.
OK, now lets pick up our heads and get out of Flatland. Imagine that the square block around Bolzano's is the set of points in the x-y plane with both x and y coordinates between 0 and 1. Divide up the square containing those points into 10 equal-sized pieces. One of those pieces has to contain infinitely many people. Suppose it is the square with bottom-left coordinates (.5, .2). Now divide that little square into 10 subsquares. Again, one of these has to contain infinitely many people. Say it is the one with lower-left coordinates (.53, .22). The picture below shows these points and a next one, say, (.537, .226). Just like the one-dimensional case, this sequence of points converges to an accumulation point (x,y) that has infinitely many people within even the smallest distance from it.
The ideas presented above are the core of one proof of the Bolzano-Weierstrass Theorem, a beautiful and very useful result in Real Analysis. The existence of the limiting values is guaranteed by the Least Upper Bound Axiom of the real numbers.
To simplify things, lets smash everything down into one dimension and pretend that the city block above is the closed interval $[0, 1]$ on the real number line. Let's represent the infinite set of people as points in this interval. Now consider the subintervals $(0, .1), (.1, .2), ... (.9, 1).$ At least one of these intervals must contain infinitely many people. Suppose, for example, that the interval $(.5, .6)$ contains infinitely people. Then split that interval into 10 segments, as shown in the picture below. At least one of these has to contain infinitely many people. Suppose, again for example, that this subinterval is $(.537, .538)$.
Now let's remove the simplification, one step at a time. First, let's see how the same construction works if in place of $[0, 1]$ we use any bounded interval $[a, b]$. Consider the function $f(x) = (x - a) / (b - a)$. That function maps $[a, b]$ onto $[0, 1]$. Its graph is a straight line with slope $1/(b - a)$. If $b - a$ is larger than 1, points get closer together when you do this mapping; otherwise they get further apart. But the expansion or contraction is by a constant factor, so the picture above looks exactly the same, just with different values for the interval endpoints. So if we do the construction inside $[0, 1]$ using the mapped points, then the pre-image of the point $r$ we end up with will be an accumulation point for the set in $[a, b]$.
OK, now lets pick up our heads and get out of Flatland. Imagine that the square block around Bolzano's is the set of points in the x-y plane with both x and y coordinates between 0 and 1. Divide up the square containing those points into 10 equal-sized pieces. One of those pieces has to contain infinitely many people. Suppose it is the square with bottom-left coordinates (.5, .2). Now divide that little square into 10 subsquares. Again, one of these has to contain infinitely many people. Say it is the one with lower-left coordinates (.53, .22). The picture below shows these points and a next one, say, (.537, .226). Just like the one-dimensional case, this sequence of points converges to an accumulation point (x,y) that has infinitely many people within even the smallest distance from it.
No comments:
Post a Comment